Dice Roller Prototype

A Unity-based turn-based dice roller inspired by Yahtzee.

Key Features

Turn-based gameplay
Dice score calculation on 3D dice objects
Yahtzee-inspired scoring system
Interactive UI for dice selection and scoring

Description

I had the idea for this spinning around in my head for a while and finally scratched the itch to make a fun prototype of it in Unity. The premise stems off trying to achieve crazy combos and attaining as high a score as you can by matching & combining dice patterns typically found in the game Yahtzee.

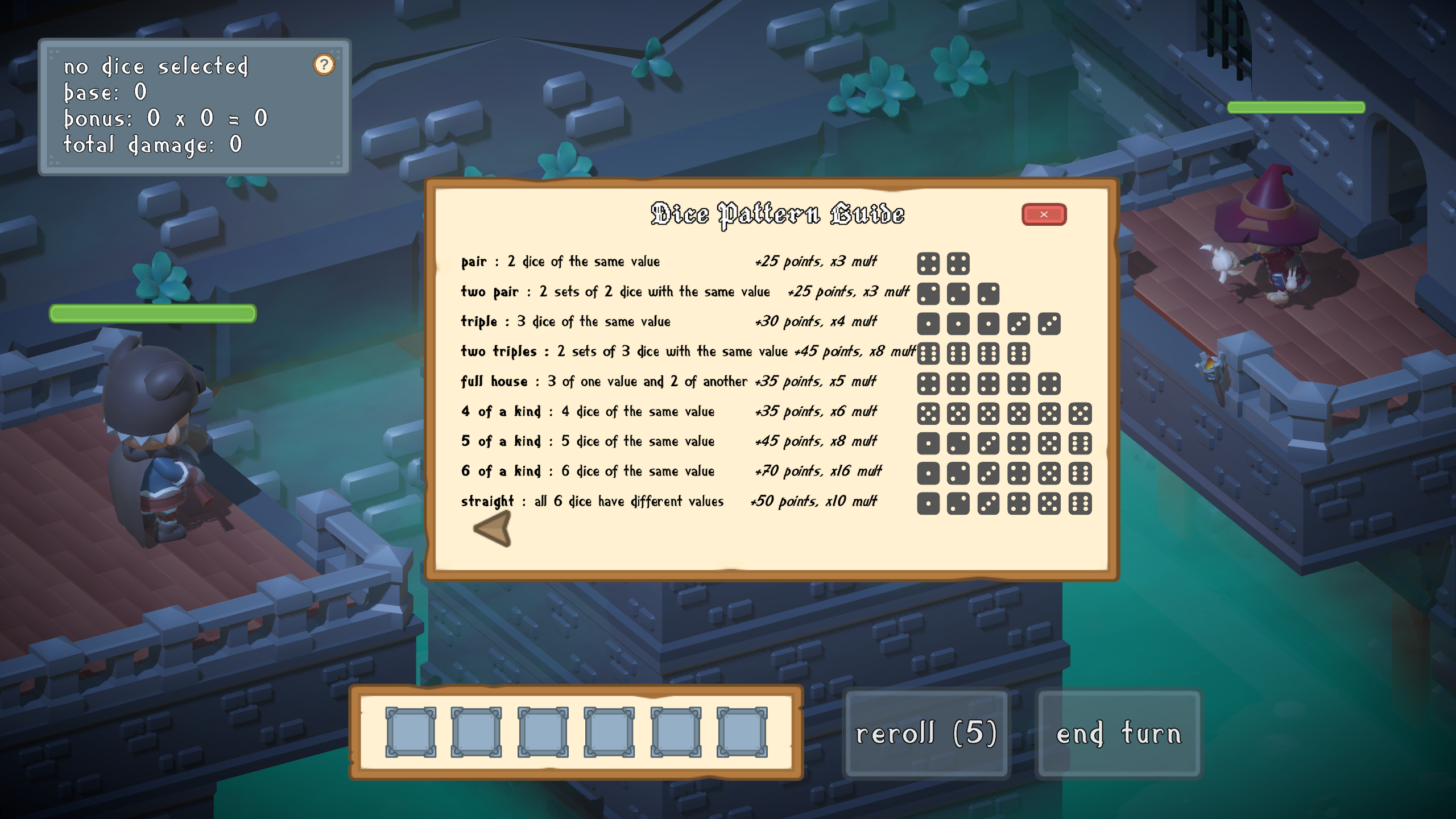
Dice Combinations and Scoring

Combination	Description	Points	Multiplier
PAIR	2 dice of the same value	+20	+2x
TWO PAIR	2 sets of 2 dice with the same value	+25	+3x
TRIPLE	3 dice of the same value	+30	+4x
TWO TRIPLES	2 sets of 3 dice with the same value	+45	+8x
FULL HOUSE	3 of one value and 2 of another	+35	+5x
4 OF A KIND	4 dice of the same value	+35	+6x
5 OF A KIND	5 dice of the same value	+45	+8x
6 OF A KIND	6 dice of the same value	+70	+16x
STRAIGHT	All 6 dice have different values	+50	+10x

For example, if a player rolls: 3, 3, 3, 4, 4, 6

This roll contains:

A Triple (three 3s): 30 points, 4x multiplier
A Pair (two 4s): 20 points, 2x multiplier

The score would be calculated as follows:

Base score from combinations: 30 + 20 = 50 points
Sum of dice face values: 3 + 3 + 3 + 4 + 4 + 6 = 23 points
Total base score: 50 + 23 = 73 points
Total multiplier: 4 + 2 = 6x
Final score: 73 * 6 = 438 points

This score of 438 points would then be dealt as damage to the enemy.

The higher the score generated, the more damage dealt to the opposing enemy. Players can choose to gamble by rerolling, in the hopes of obtaining a die to make a higher-tiered combination, thus dealing more damage to their opponent.

The gameplay loop works via turn-based combat in which the player has a limited number of rerolls, but can gain an extra roll per enemy kill. At the end of the turn, the score generated is dealt to the enemy as damage. The enemy will then retaliate with an attack of their own (if still alive). This repeats until all enemies are defeated or the player loses all their health.

Balancing Probabilities and Points

An essential aspect of the game's design is balancing the points based on the probability of achieving different patterns. To ensure fair and engaging gameplay, I developed a Python script to simulate dice rolls and calculate the probabilities of each pattern occurring within a given number of rolls.

This simulation helped me make informed decisions about adjusting the scoring system:

Increased the reward for harder-to-achieve patterns like 6 OF A KIND and TWO TRIPLES, as they occur less frequently than I initially thought they did.
Slightly reduced the scoring for more common patterns like FULL HOUSE and 4 OF A KIND to balance their frequency.
Adjusted STRAIGHT to be valuable but not overvalued, considering its rarity.
Kept PAIR and TWO PAIR relatively low as they're common in early rolls.
Slightly reduced 5 OF A KIND's scoring as it becomes quite common in later rolls.

View Probability Simulation Script


import random
from collections import Counter

def roll_dice(num_dice=6):
    return [random.randint(1, 6) for _ in range(num_dice)]

def identify_pattern(dice):
    counts = Counter(dice)
    sorted_counts = sorted(counts.values(), reverse=True)
    
    if sorted_counts[0] == 6:
        return "6 OF A KIND"
    elif sorted_counts[0] == 5:
        return "5 OF A KIND"
    elif sorted_counts[0] == 4:
        return "4 OF A KIND"
    elif sorted_counts == [3, 3]:
        return "TWO TRIPLES"
    elif sorted_counts[:2] == [3, 2]:
        return "FULL HOUSE"
    elif sorted_counts[0] == 3:
        return "TRIPLE"
    elif sorted_counts[:2] == [2, 2]:
        return "TWO PAIR"
    elif sorted_counts[0] == 2:
        return "PAIR"
    elif len(counts) == 6:
        return "STRAIGHT"
    else:
        return "NO PATTERN"

def get_dice_to_reroll(dice, pattern):
    counts = Counter(dice)
    if pattern == "6 OF A KIND":
        return []
    elif pattern == "5 OF A KIND":
        return [i for i, val in enumerate(dice) if val != counts.most_common(1)[0][0]]
    elif pattern == "4 OF A KIND":
        most_common = counts.most_common(1)[0][0]
        return [i for i, val in enumerate(dice) if val != most_common]
    elif pattern == "TWO TRIPLES":
        return [i for i, val in enumerate(dice) if counts[val] != 3]
    elif pattern == "FULL HOUSE":
        most_common = counts.most_common(1)[0][0]
        return [i for i, val in enumerate(dice) if counts[val] != 3]
    elif pattern == "TRIPLE":
        most_common = counts.most_common(1)[0][0]
        return [i for i, val in enumerate(dice) if val != most_common]
    elif pattern == "TWO PAIR":
        pairs = [val for val, count in counts.items() if count == 2]
        return [i for i, val in enumerate(dice) if val not in pairs]
    elif pattern == "PAIR":
        most_common = counts.most_common(1)[0][0]
        return [i for i, val in enumerate(dice) if val != most_common]
    elif pattern == "STRAIGHT":
        return [random.randint(0, 5)]  # Reroll one random die
    else:
        return list(range(6))  # Reroll all dice

def simulate_rolls(num_simulations, max_rolls):
    patterns = {
        "6 OF A KIND": 0,
        "5 OF A KIND": 0,
        "4 OF A KIND": 0,
        "TWO TRIPLES": 0,
        "FULL HOUSE": 0,
        "TRIPLE": 0,
        "TWO PAIR": 0,
        "PAIR": 0,
        "STRAIGHT": 0,
        "NO PATTERN": 0
    }
    pattern_order = list(patterns.keys())
    
    for _ in range(num_simulations):
        dice = roll_dice()
        best_pattern = "NO PATTERN"
        for _ in range(max_rolls):
            pattern = identify_pattern(dice)
            if pattern_order.index(pattern) < pattern_order.index(best_pattern):
                best_pattern = pattern
            if best_pattern == "6 OF A KIND":
                break
            dice_to_reroll = get_dice_to_reroll(dice, best_pattern)
            for index in dice_to_reroll:
                dice[index] = random.randint(1, 6)
        patterns[best_pattern] += 1
    
    return patterns

def calculate_probabilities(patterns, num_simulations):
    return {pattern: count / num_simulations * 100 for pattern, count in patterns.items()}

def main():
    num_simulations = 100000
    max_rolls_list = [1, 2, 3, 4, 5]
    
    for max_rolls in max_rolls_list:
        print(f"\nSimulating {num_simulations} games with up to {max_rolls} rolls each...")
        patterns = simulate_rolls(num_simulations, max_rolls)
        probabilities = calculate_probabilities(patterns, num_simulations)
        
        print(f"\nProbabilities of achieving each pattern within {max_rolls} rolls:")
        for pattern, probability in sorted(probabilities.items(), key=lambda x: x[1], reverse=True):
            print(f"{pattern:<12}: {probability:.2f}%")

if __name__ == "__main__":
    main()

Technical Challenges

One challenge I faced was determining which face of each die was facing up to attribute the correct score. While this task is straightforward for humans, implementing it in code proved to be an interesting challenge. I solved this by using a trigger collider on each face of the dice and a face detector script attached to the floor where the dice land. Once a die's velocity settles and it comes to rest, the detector activates and determines which collider it contacts. Each face is mapped to a corresponding trigger collider, returning a value attributed to the die object.

Using colliders works well for this small prototype, but a more performant method would map the rotation values of the dice to associated face values and check the die's current rotation when stationary. I initially attempted this approach, but for whatever reason the results lacked consistency. Considering the time constraints of a prototype, I decided to move away from this method and instead employ the aforementioned approach.

These adjustments helped create a more balanced and rewarding gameplay experience, encouraging players to aim for rarer patterns while still valuing more common combinations.

Tools Used

Languages: C#

Software: Unity

Code

View On GitHub

Play

Play On Itch.io